Tenemos el siguiente problema:
Las alturas de los alumnos de una clase siguen una distribución normal de media 170cm y desviación típíca 9 cm. Calcula la probabilidad de que al escoger un alumno al azar su altura:
i) Sea menor que 1.74 m ii) Sea mayor que 1.79 miii) Sea menor que 1.65 m iv) Sea mayor que 1.68 m
v) Esté entre 1.74 m y 1.79 m vi) Esté entre 1.68 m y 1.72 m
vii) Este entre 1.65 m y 1.69 m
La solución utilizando tablas:
La solución usando WolframAlpha:
Para hallar la probabilidad de una variable aleatoria con distribución normal, tenemos que usar la siguiente instrucción: probability variable , normal distribution, mean=valor, sd=valor . Entonces resolvemos el ejercicio anterior:
i) Sea menor que 1.74 m.
En WolframAlpha: probability X<174 , normal distribution, mean=170, sd=9
ii) Sea mayor que 1.79 m.
En WolframAlpha: probability X>179 , normal distribution, mean=170, sd=9
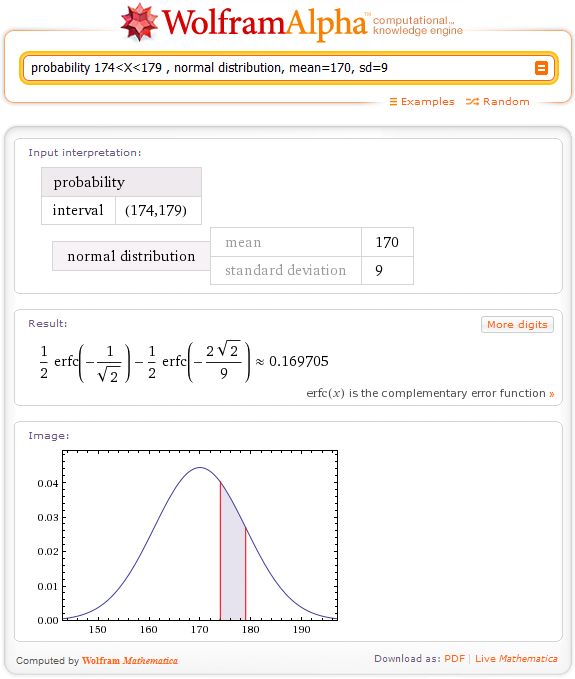
v) Esté entre 1.74 m y 1.79 m
En WolframAlpha: probability 174< X <179Página de Wolfram Alpha


La probabilidad que ocurran ambos es 0.02, la probabilidad de que ocurra B es 0.4
ResponderEliminarLa probabilidad de que al menos uno ocurra es 0.9. Encuentre la probabilidad de:
a) A
b)Sòlo B
c) Ninguno ocurra
d) Si B ocuure ¿Cuàl es la probabilidad de A?
e)No ocurre A.