Examen Admisión San Marcos 2016-I - Solucionario UNMSM

 
SOLUCIONARIO DEL EXAMEN DE ADMISIÓN A LA UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS UNMSM 2016-1 

PREGUNTAS DE RAZONAMIENTO MATEMATICO - ADF.
PREGUNTA 1
Se tiene 12 barras de chocolate, de las cuales 4 están enumeradas con el número 6; 4 con el número  5 y 4 con el número 1. Se distribuye las 12 barras en tres bolsas, A, B y C con igual número de barras. Si la suma de los números de la bolsa A es igual a 19, la de B es igual a 17 y la de C es igual a 12,  entonces es cierto que la bolsa C tiene:
A) Tres barras con el número 1.                   B) Dos barras con el número 6.
C) Dos barras con el número 1.                   D) Ninguna barra con el número 5.
E) Una barra con el número 6.



PREGUNTA 2
José agrupa sus canicas secuencialmente tal como se muestra en la figura. Siguiendo la misma secuencia,  ¿cuántas canicas tendrá el vigésimo grupo?
A) 2²⁰          B) 2²⁰ + 1            C) 2¹⁹ + 1            D) 2²⁰ − 1              E) 2¹⁹ − 1

PREGUNTA 3
Seis  amigos  se  ubican  simétricamente  alrededor de una mesa circular para almorzar. Si se sabe que
 - Alex no está al lado de Joel ni de Daniel.
 - Aldo no está al lado de Alex ni de Oliver.
 - Daniel no está al lado de Joel ni de Oliver.
 - Nilo está junto y a la derecha de Alex.
¿Quién está junto y a la izquierda de Daniel?
A) Alex     B) Nilo    C) Aldo     D) Joel    E) Oliver

PREGUNTA 4
Un lector, por accidente, arranca algunas hojas de su libro, por este motivo no quedan en  el libro las páginas: 30, 47, 48, 54, 56, 121, 122, 198 y 199. Si el libro tenía 100 hojas,  ¿cuántas hojas le quedan ahora?
A) 94       B) 92       C) 7        D) 91        E) 93

PREGUNTA 5
Cinco mujeres, al ser interrogadas por un delito que cometió una de ellas, manifestaron lo siguiente:
- Bertha: Fue Elsa
- Ana: Fue Bertha
- Elsa: Bertha miente
- María: Yo no fui
- Karla: Yo fui
Si solo una de ellas dice la verdad, ¿quién cometió el delito?
A) Bertha        B) Ana         C) María         D) Elsa        E) Karla



PREGUNTA 6
Si a, b, c, d, e, f, g representan dígitos diferentes y pertenecen al conjunto {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, tal que:

Si (efg) es el mayor resultado que se puede obtener en la operación, halle la suma de los dígitos que no se  usaron en la operación.
A) 7        B) 8        C) 9        D) 6       E) 5



PREGUNTA 7
Se tiene un terreno rectangular cuyas dimensiones de largo y ancho están en relación de 2 a 1 y su  perímetro mide 54 m. Para cercar con mallas este terreno, se colocan postes (verticalmente) a lo largo del  perímetro a una  distancia de 90 cm uno del otro. ¿Cuántos postes son necesarios para cercar el terreno?
A) 56      B) 59      C) 58      D) 60      E) 62

PREGUNTA 8
Sea N el mayor número entero con cifras diferentes, ninguna de ellas cero y es múltiplo de 36.  ¿Cuál es la cifra de decenas de N?
A) 4         B) 3          C) 2         D) 5         E) 1

PREGUNTA 9
Las edades de Julio y su padre difieren en 24 años. Si Julio nació en el año (19ab) y en 1980  tuvo (a+b) años, ¿en qué año ambas edades sumaron 112 años?
A) 2011       B) 2012        C) 2013       D) 2014      E) 2010

PREGUNTA 10
De un grupo de 50 estudiantes que aprobaron el curso de Aritmética o el curso de Álgebra, se sabe  que el número de mujeres que aprobaron solo Álgebra es la quinta parte del número de mujeres que  aprobaron solo Aritmética. El número de estudiantes que aprobaron Aritmética y Álgebra excede en  5 al número de estudiantes hombres que aprobaron solo Aritmética y este último es igual al número  de estudiantes hombres que aprobaron solo Álgebra. ¿Cuál es la mínima cantidad de estudiantes que aprobaron solo Álgebra?
A) 6       B) 8       C) 7       D) 5       E) 9

PREGUNTA 11
Por 12 horas de trabajo, a un operario se le promete pagar $100 y un regalo. El operario se retiró  luego de 8 horas de trabajo, por lo que recibió $60 más el regalo. ¿Cuál es el valor del regalo?
A) $ 30         B) $ 40         C) $ 20         D) $ 50        E) $ 10

PREGUNTA 12
De cierto número de problemas, Roberto resuelve el primer día 3/10  del total y en el segundo día  resuelve 5/7  de lo que le faltaba resolver, lo que es igual a 50 problemas. ¿Cuántos problemas le  faltan resolver?
A) 20       B) 30      C) 50        D) 10      E) 15

PREGUNTA 13
La edad actual de Pedro es seis veces la de Ana. Luis y Ana tienen juntos 20 años, y la edad de Luis es el  doble de la edad de Ana, más 2 años. Halle la edad que Pedro tendrá dentro de 5 años.
A) 54 años         B) 30 años          C) 21 años
D) 69 años         E) 41 años

PREGUNTA 14
Sean las cantidades positivas A, B y C. El producto de A y B es igual a  1/4 C. Si A aumenta en un 60%  y B disminuye en un 25%, ¿en qué porcentaje debe aumentar C para que se mantenga la igualdad?
A) En un 25%        B) En un 20%           C) En un 30%
D) En un 15%        E) En un 22%



PREGUNTA 15
Si f(x+1) = x(x+2), ¿cuál es el valor de f(x) – f(x+2)?
A) –4(x+1)          B) (x+1)(x+3)          C) (x–1)(x+1)
D) 4(x–1)            E) (x–1)(x+3)

PREGUNTA 16
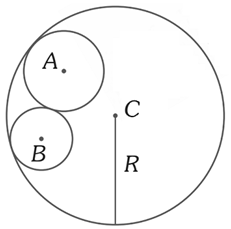
En la figura, los puntos A, B y C son centros de las circunferencias tangentes, donde R=10 cm.  Halle el semiperímetro del triángulo formado al unir A, B y C.
A) 8 cm          B) 12 cm           C) 14 cm
D) 6 cm          E) 10 cm

PREGUNTA 17
En la figura, ABCD es un rectángulo, AB = 6 cm  y BC = 9 cm. Calcule el área de la región sombreada.
A) 98/5 cm²              B) 97/5 cm²              C) 101/5 cm² 
D) 99/5 cm²              E) 18cm²

PREGUNTA 18
En la figura,  AB=DC. Calcule la medida del ángulo AB ̂D.
A) 20°       B) 30°       C) 25°      D) 40°      E) 35°

PREGUNTA 19
En la figura, P es punto medio de (BC); (RS)//(AD) y  (CS) = 2(DS). ¿Qué fracción del área del cuadrado ABCD  es el área de la región?
A) 2/15      B) 3/16          C) 3/4       D) 1/4        E) 5/16

PREGUNTA 20
En la figura, los vértices B,C y D del cuadrado ABCD son centros de los arcos de circunferencias. Si AB=4 cm y T es punto de tangencia, halle el área de la región sombreada.

SOLUCIONARIOS DEL EXAMEN DE ADMISIÓN SAN MARCOS 2016.

PREGUNTAS DE RAZONAMIENTO MATEMATICO - BCE.
PREGUNTA 1
El gráfico muestra cinco barriles de vino y uno de pisco, con su respectiva cantidad de litros y no  necesariamente en ese orden. Un comerciante vende, el primer día, cierto número de litros de vino;  el segundo día, el doble de litros de vino que el primer día, quedándose con todo el pisco y sin vino.  ¿Cuántos litros tiene el barril de pisco?
A) 19        B) 20            C) 18          D) 16          E) 15

 

PREGUNTA 2
En cada una de las casillas de la figura se escribe un número diferente. El producto de los números  que están en las casillas a, b y c es 84; el producto de los números que están en las casillas b, c y d es  140; el producto de los números que están en las casillas c, d y e es 280; y el producto de los números  que están en las casillas d, e y f es 600. Halle la suma de los números que deben ir en las casillas b y e.
A) 12      B) 18       C) 19         D) 15         E) 13

 

PREGUNTA 3
En el siguiente cuadro, escriba los números del 3 al 11, sin que alguno se repita, de tal manera que la suma de los tres números que forman filas, columnas y diagonales sea la misma. Halle el valor de m.
A) 6       B) 5       C) 8        D) 7       E) 9

PREGUNTA 4
En la secuencia mostrada, ¿cuántas figuras geométricas de forma cuadrada hay en el gráfico N.º 10? A) 285        B) 385        C) 383         D) 387            E) 389

>> SOLUCIÓN     


PREGUNTA 5
La figura muestra tres frascos que contienen caramelos: uno tiene solo caramelos de limón, otro tiene  solo de fresa y el restante los tiene de ambos sabores. Ningún frasco está correctamente rotulado.  ¿Cuántos caramelos como mínimo y de qué frasco o frascos se debe sacar para poder rotularlos  correctamente?

A) 1 caramelo del frasco rotulado limón.
B) 1 caramelo del frasco rotulado fresa.
C) 1 caramelo del frasco rotulado limón y otro del fresa.
D) 1 caramelo del frasco rotulado fresa y otro del mezcla.
E) 1 caramelo del frasco rotulado mezcla.

PREGUNTA 6
De un total de 120 personas encuestadas, 25 personas hablan inglés y francés, 40 solo hablan francés  y 20 no hablan ninguno de estos idiomas.  Obtenga el número de personas que habla solo uno de estos idiomas.
A) 65       B) 75        C) 85        D) 80      E) 70

PREGUNTA 7
La estatura promedio de todos los estudiantes en un salón del tercer grado es de 1 metro.  Si la estatura promedio de los varones que son en total 10 es de 1,15 m y la estatura  promedio de todas las mujeres es 0,90 m. Halle el número de estudiantes en el salón.
A) 25      B) 15       C) 28        D) 22       E) 14

PREGUNTA 8
A pedido de un supermercado, un banco envía 360 monedas de 10 céntimos, 648 monedas de 20 céntimos y  432 monedas de 50 céntimos. Dichas monedas se agruparon en varias bolsas, de modo tal que cada bolsa  tenía el mismo número de monedas y de igual denominación.
¿Cuál es el mayor número de monedas que se colocaron en cada bolsa?
A) 108        B) 36          C) 18          D) 24        E) 72

PREGUNTA 9
Para realizar un viaje al extranjero, una agencia de turismo ofrece:
 - Pasajes de ida y vuelta a $ 4250 por persona.
 - Alojamiento individual a $ 85 por día.
 - Alimentación a $ 115 por persona y por día.
¿Cuál es el presupuesto necesario para 4 personas durante 5 días con el 10% de descuento  en el rubro de pasajes?
A) $ 16 100      B) $ 18 300      C) $ 19 300        D) $ 27 000       E) $ 18 800

PREGUNTA 10
A un paciente se le receta tomar una pastilla del tipo A cada 8 horas y dos pastillas del tipo B cada 7 horas.  Si empieza su tratamiento tomando los dos tipos de pastillas simultáneamente, ¿en cuántas horas como  mínimo habrá tomado 18 pastillas?
A) 35          B) 42         C) 32        D) 56         E) 40

PREGUNTA 11
Janeth, que dispone de una cantidad de dinero para comprar chocolates, les dijo a sus sobrinos:  “Si compro tres chocolates para cada uno de ustedes, me sobraría dinero exactamente para cuatro  chocolates más, pero si quisiera comprar cuatro chocolates para cada uno de ustedes, me faltaría  exactamente el dinero para tres chocolates más”. ¿Cuántos sobrinos tiene Janeth?
A) 6           B) 5           C) 4          D) 7         E) 8

PREGUNTA 12

PREGUNTA 13
Los precios de una pulsera y un reloj son, respectivamente, 20 y 15 dólares. Si María gasta $250  en comprar 14 artículos entre pulseras y relojes, ¿cuál es la diferencia positiva del número de  dichos artículos?
A) 2            B) 8           C) 4           D) 6           E) 3

PREGUNTA 14
Cada fin de semana, Pedro viaja a Ica o a Piura. El pasaje de ida y vuelta a Piura cuesta S/.240 y el  de ida y vuelta a Ica cuesta la mitad. Si en las últimas 9 semanas ha gastado en pasajes S/.1200,  ¿cuántas veces viajó y volvió de Ica?
A) 6          B) 4         C) 7         D) 5          E) 8

PREGUNTA 15
Las edades de Ana y Juan hace x años eran 8 y 12 años respectivamente. Dentro de x años serán 28 y 32  años respectivamente. ¿Cuál es la edad actual de Juan?
A) 22 años        B) 18 años          C) 32 años         D) 20 años      E) 24 años

PREGUNTA 16
Se desea cubrir toda la región sombreada conformada por dos rectángulos con losetas de 20 cm × 20 cm.  Si cada loseta cuesta 10 dólares, ¿cuál será el costo total de las losetas?
A) $ 4200       B) $ 4250        C) $ 3800       D) $ 4500       E) $ 4120

PREGUNTA 17
Un agricultor tiene un campo para cultivar frutas que ha sido dividido en cinco parcelas, tal como muestra la figura. Las parcelas I, II, III y IV son regiones cuadradas. Además, las parcelas IV y V forman un cuadrado. Si el área de la parcela I es 25 m², el área de la parcela II es 49 m² y el área de la parcela IV es 81 m², halle el área de la parcela V.
A) 441m²        B) 333 m²      C) 396 m²        D) 360 m²       E) 400 m²

PREGUNTA 18
De una lámina de 10 cm de ancho y 14 cm de largo se construye una caja abierta, cortando un cuadrado  de 2 cm de lado en cada esquina. El volumen de la caja resultante es:
A) 100 cm³         B) 120 cm³        C) 125 cm³        D) 150 cm³       E) 80 cm³

PREGUNTA 19
En la figura, D es punto medio de AC. Halle el valor de x.
A) 45°        B) 15°         C) 20°          D) 25°        E) 30°

Solucionario del Examen de Admisión a San Marcos 2016-I

► Recopilación de examenes de admisión pasados a la Universidad Nacional Mayor de San Marcos UNMSM