Wolfram|Alpha es un "computational knowledge engine"(motor de conocimiento computacional), algo así como google (le podemos hacer consultas sobre preguntas), pero a diferencia de google, Wolfram|Alpha no devuelve links sino que da la respuesta directa a la consulta que se le hace. Wolfram|Alpha puede dar respuestas precisas en muchos campos del conocimiento, su fuerte son las matemáticas, en este post veremos como utilizarlo para hallar la solución analítica (con procedimiento) y gráfica de muchos tipos de ecuaciones diferenciales, veamos algunos ejemplos:
Ecuaciones Diferenciales de Primer Orden
Ecuaciones de Variables separables
Resolver:
Primero ingresamos a la pagina de WolframAlpha y escribimos en la caja de texto lo siguiente:
solve dy/dx = cos(2x)
También se puede ingresar el diferencial dy/dx como y', entonces la ecuación anterior la escribimos como:
solve y' = cos(2x)
Luego Wolfram|Alpha nos mostrará la siguiente información: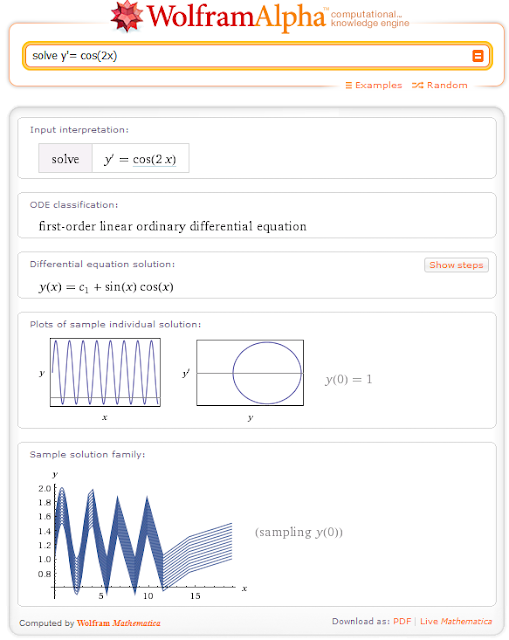
En la primera parte se puede verificar si lo ingresado corresponde con la ecuación que necesitamos resolver, a veces por problemas de paréntesis ó de símbolos las ecuaciones que ingresamos Wolfram|Alpha las interpreta de diferente manera; luego nos aparece la clasificación de la ecuación, su solución analítica y un gráfico de la solución para un valor inicial supuesto y también un gráfico de la familia de soluciones.
Veamos más ejemplos:
Resolver:
Ingresamos lo siguiente: (el logaritmo natural ln, en Wolfram Alpha se ingresa como log)
solve y log(x) dy/dx = ((y+1)/x)^2

Si queremos ver el procedimiento, sólo tenemos que hacer click en "Show Steps"

Ecuaciones Homogéneas
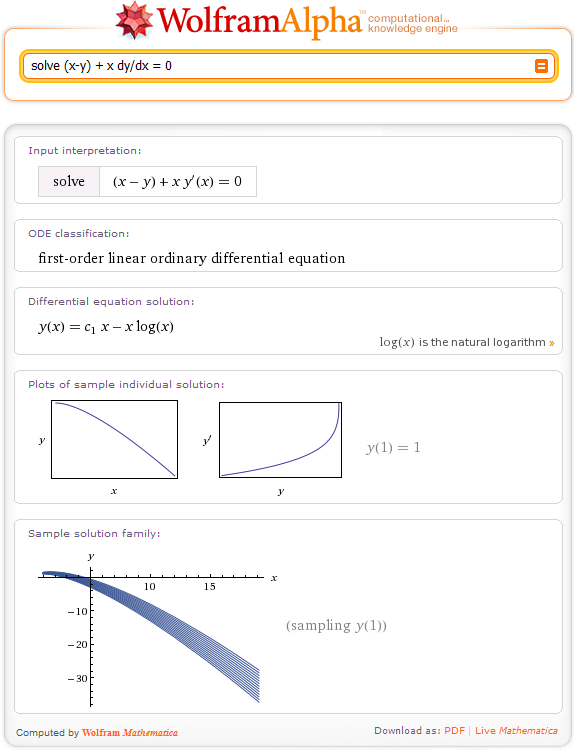
Resolver:Ingresamos lo siguiente:
solve (x-y) + x y' = 0
Ecuaciones Exactas.
Resolver: Ingresamos lo siguiente:
solve (siny - y sinx) + (cosx + x cosy - y) y'= 0
Ecuaciones de Bernoulli, Ricatti y Clairaut.
Resolver:Ingresamos lo siguiente:
solve y'- y = exp(x) y^2
Ecuaciones con valor inicial. (Método de Picard)
Resolver: Ingresamos lo siguiente:
solve y'+2xy=x, y(0)=0
Ecuaciones de Segundo Orden
Resolver: Se debe ingresar:
solve: y''-4y'+4y=(x+1)*exp(2x)
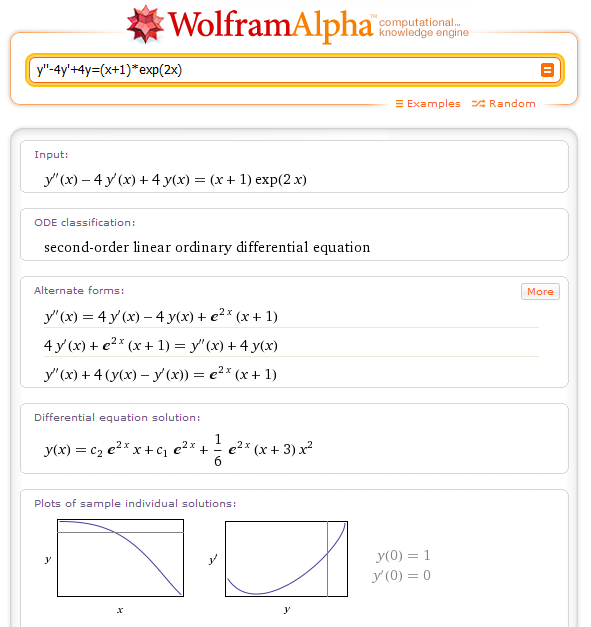
Solución de ecuaciones diferenciales utilizando el Método de Laplace.
Resolver: y''(t) - 2y'(t) + t y(t) = 0, y(0) = 0
Se debe ingresar: solve t y''(t) - 2y'(t) + t y(t) = 0, y(0) = 0
Relacionado:
Ecuaciones Diferenciales de Ordinarias de Primer Orden - Teoría y Ejercicios Resueltos
Otras capacidades de WolframAlpha, en palabras de su creador Stephen Wolfram:
Tema: pagina para resolver ecuaciones diferenciales, solucionador de ecuaciones diferenciales online, ecuaciones diferenciales online.









calculo de aresa con integrales
ResponderEliminarpero yo necesito resolver digamos ver todos los pasos para resolver ejercicios de ecuaciones diferenciales ya sean variables separables, homogeneas, exactas o de factor integrante
ResponderEliminarSuponga que la admision a una universidad satisface el modelo de ley logistica. Si hace 5 años la admision era 10000 y si la admision ahora es 15000 y si la maxima admision de la universidad es 25000, ¿cuando llegara a la admision a 18000, 21000 y 24000?
ResponderEliminarando en los mismos aprietos de modelos logísticos
Eliminarando en los mismos aprietos de modelos logísticos
ResponderEliminarcomo sacar el factor integrante?
ResponderEliminar(2xy)dx+(y^2-3x^2 )dy=0 es una ecuacion diferencial homogenea AYUDA!!!
ResponderEliminares algo compleja esta ecuacion diferencial, la solución requiere tiempo con la versión pro
Eliminar