EJERCICIO #1
Una
panadería es famosa por su dos especialidades de tartas: la tarta Imperial y
la tarta de Lima. La tarta Imperial requiere para su elaboración medio kilo
de azúcar y 8 huevos y tiene un precio de venta de 8 €. La tarta de Lima
necesita 1 kilo de azúcar y 8 huevos, y tiene un precio de venta de 10 €. En
el almacén les quedaban 10 kilos de azúcar y 120 huevos.
a)
¿Qué combinaciones de especialidades pueden hacer?. Plantea el problema y representa gráficamente el conjunto de
soluciones.
b)
¿Cuántas unidades de cada especialidad han de producirse para obtener el
mayor ingreso por ventas?
EJERCICIO #2
Un orfebre fabrica dos tipos de joyas. La unidad del tipo A se hace con 1 g de oro y 1,5 g de plata y se vende a 25 €. La de tipo B se vende a 30 € y lleva 1,5 g de oro y 1 g de plata. Si solo dispone de 750 g de cada metal, ¿cuántas joyas ha de fabricar de cada tipo para obtener el máximo beneficio?
EJERCICIO #3
Un comerciante acude a cierto mercado a comprar naranjas con 500 €. Le
ofrecen dos tipos de naranjas: las de tipo A a 0,5 € el kg y las de tipo B a
0,8 € el kg. Sabemos que solo dispone en su furgoneta de espacio para
transportar 700 kg de naranjas como máximo y que piensa vender el kilo de
naranajas de tipo A a 0,58 € y el de tipo B a 0,9 €.
¿Cuántos kilogramos de naranjas de cada tipo deberá comprar para obtener
beneficio máximo?
EJERCICIO #4
Un veterinario aconseja a un granjero dedicado a la cría de aves una dieta mínima que consiste en 3 unidades de hierro y 4 unidades de vitaminas diarias. El granjero sabe que cada kilo de maíz proporciona 2,5 unidades de hierro y 1 de vitaminas y que cada kilo de pienso compuesto proporciona 1 kilo de hierro y 2 de vitaminas. Sabiendo que el kilo de maíz vale 0,3 € y el de pienso compuesto 0,52 €, se pide:
a) ¿Cuál es la composición de la dieta diaria que minimiza los costes del granjero? Explica los pasos seguidos para obtener la respuesta.
b) ¿Cambiaría la solución del problema si por escasez en el mercado el granjero no pudiera disponer de más de 1 kilo diario de pienso compuesto?.
EJERCICIO #5
Se va a organizar una planta de un taller de automóviles donde van a
trabajar electricistas y mecánicos. Por necesidades del mercado, es necesario
que haya mayor o igual número de mecánicos que de electricistas y que el
número de mecánicos no supere al doble que de electricistas. En total hay
disponibles 30 electricistas y 20 mecánicos.
El beneficio de la empresa
por jornada es de 150 € por electricista y 120 € por mecánico.
¿Cuántos trabajadores de cada clase deben elegirse para obtener el máximo
beneficio?
EJERCICIO #6
Un ganadero debe suministrar un mínimo diario de 4 mg de vitamina A y 6
mg de vitamina B en el pienso que da a sus reses. Dispone para ello de dos
tipos de pienso P y P , cuyos contenidos vitamínicos por kg son los que
aparecen en la tabla:
Si el kilogramo de pienso P1 2 vale 0,4 € y el del P vale 0,6 €,
¿cómo deben mezclarse los piensos para suministrar las vitaminas requeridas
con un coste mínimo?

EJERCICIO #7
Un taller de confección hace chaquetas y pantalones para niños. Para
hacer una chaqueta, se necesitan 1 m de tela y 2 botones; y para hacer unos
pantalones, hacen falta 2 m de tela, 1 botón y 1 cremallera. El taller dispone
de 500 m de tela, 400 botones y 225 cremalleras. El beneficio que se obtiene
por la venta de una chaqueta es de 20 €, y por la de unos pantalones, 30 €.
Suponiendo
que se vende todo lo que se fabrica, calcula el número de chaquetas y de
pantalones que se tienen que hacer para obtener un beneficio máximo.
EJERCICIO #8
Una persona tiene 15.000 € para invertir en dos tipos de acciones, A y
B. El tipo A tiene un interés anual del 9%, y el tipo B, del 5%. Decide
invertir, como máximo, 9.000 € en A, y como mínimo, 3.000 € en B. Además,
quiere invertir en A tanto o más que en B.
a)
Dibuja la región factible.
b)
¿Cómo debe invertir los 15.000 € para que el beneficio sea máximo?
c) ¿Cuál es ese beneficio anual máximo?
EJERCICIO #9
Una empresa que sirve comidas preparadas tiene que diseñar un menú
utilizando dos ingredientes. El ingrediente A contiene 35 g de grasas y 150
Kilo calorías por cada 100 g de ingrediente, mientras que el B contiene 15 g
de grasas y 100 Kilo calorías por cada 100 g. El coste es de 1,5 euros por
cada 100 g. del ingrediente A y de 1 euros por cada 100 g del ingrediente
B.
El menú a diseñar debería contener no más de 30 g de grasas y al menos
110 Kilo calorías por cada 100 g de alimento. Se pide determinar las
proporciones de cada ingrediente a emplear en el menú de manera que su coste
sea lo más reducido posible.
1. Indique la expresión de las restricciones y la función
objetivo.
2. Represente gráficamente la región delimitada por las restricciones.
3. Calcule el porcentaje óptimo de cada ingrediente a incluir en el
menú.
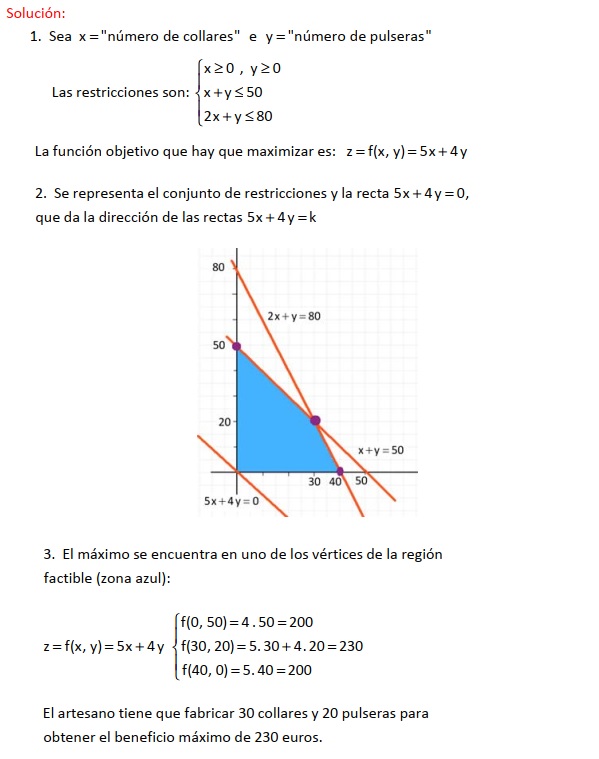
EJERCICIO #10
Un artesano fabrica collares y pulseras. Hacer un collar le lleva dos
horas y hacer una pulsera una hora. El material de que dispone no le permite
hacer más de 50 piezas.
Como mucho, el artesano puede dedicar al trabajo
80 horas. Por cada collar gana 5 euros y por cada pulsera 4 euros. El artesano
desea determinar el número de collares y pulseras que debe fabricar para
optimizar sus beneficios.
1. Exprese la función objetivo y las
restricciones del problema.
2. Represente gráficamente el recinto
definido.
3. Obtenga el número de collares y pulseras correspondientes al
máximo beneficio.
EJERCICIOS RESUELTOS DE PROGRAMACIÓN LINEAL












Hola tengo una pregunta si en las ecuacion es por ejemplo x1-x2 y la otra 2x1-3x2 la grafica saldria del lado negativo del plano ??? o seria igual como la del video del lado positivo?
ResponderEliminarQue estúpido cualquiera se sabe eso
Eliminardesconocer algo de programacion lineal o de matematicas no te convierte en estupido, de donde sacas esas ideas?, me parece has tenido un mal dia.
Eliminarkawai
ResponderEliminarMuchas gracias desde España! Estoy haciendo empresariales y quería felicitarte porque ha sido super sencillo explicado, lo he entendido todo a la primera.
ResponderEliminarGracias!
ResponderEliminarcomo esta profesor.., DÉJEME FELICITARLE POR UNA EXPLICACIÓN CLARA..ahora usted mismo me puede decir como resolver este ejercicio, con el método gráfico: x/2+y/3=9
x +y =21
le agradeceré por el apoyo.
ALGUIEN QUE ME PUEDA AYUDAR A RESOLVER ESTE EJERCICIO DE PROGRAMACIÓN LINEAL.
ResponderEliminarUna planta inyectora de artículos plásticos produce dos modelos de un accesorio para
refrigeradores. El modelo A requiere para su
producción
3 horas/maquina por cada 100
unidades. El modelo B requiere solo 1 horas/maquina por cada 100 unidades. Se
dispone
en el mes, 171 horas/maquina.
El departamento de ventas informa que durante el próximo mes
se requerirán 4000
unidades del producto A y 12000 unidades del producto B.
Si la utilidad neta producida por una unidad de A es de $ 2.00 y la producida por una
unidad de B es de $ 1.40 ¿Qué cantidad mensual debe producirse de A y de B, con el
objeto de maximizar la utilidad
?
Utilizar el método
gráfico
nel
EliminarALGUIEN QUE ME PUEDA AYUDAR A RESOLVER ESTE EJERCICIO DE PROGRAMACIÓN LINEAL.
ResponderEliminarUna planta inyectora de artículos plásticos produce dos modelos de un accesorio para
refrigeradores. El modelo A requiere para su
producción
3 horas/maquina por cada 100
unidades. El modelo B requiere solo 1 horas/maquina por cada 100 unidades. Se
dispone
en el mes, 171 horas/maquina.
El departamento de ventas informa que durante el próximo mes
se requerirán 4000
unidades del producto A y 12000 unidades del producto B.
Si la utilidad neta producida por una unidad de A es de $ 2.00 y la producida por una
unidad de B es de $ 1.40 ¿Qué cantidad mensual debe producirse de A y de B, con el
objeto de maximizar la utilidad
?
Utilizar el método
gráfico
X1= número de artículos a fabricar del modelo A
EliminarX2= número de artículos a fabricar del modelo B
la funcion objetivo es:
Maximizar Z= 2 X1 + 1.4 X2
sujeto a las siguientes restricciones:
3X1 + X2<=171 restriccion1
X1<=40 restriccion2
X2<=120 restriccion3
X1,X2 >=0 restricciones de no negatividad
4000/100 4000 unidades del producto A /100 unidades fabricadas por la maquina =40
12000/100 12000 unidades del producto B /100 unidades fabricadas por la maquina =120
Restriccion 1 3X1 + X2 <=171
se iguala
3X1 + X2 =171 3X1 + X2 =171
se da valor a X1=0 se da valor a X2=0
3(0) + X2 =171 3X1 + (0) =171
X2=171 X1=171/3 X1=57
coordenada:(0,171) coordenada:( 57, 0)
Restricción 2 X1 <=40
se iguala
X1 =40 por lo tanto X2 vale 0; la linea recta solo pasa por el eje x
Restricción 2 X2 <=120
se iguala
X2 =120 por lo tanto X1 vale 0 la linea recta solo pasa por el eje y
posteriormente se grafica, se observan los vértices y sus coordenadas
Vértice 1 = (0,120)
Vértice 2 = (17,120)
Vértice 3 = (40,51)
Vértice 4 = (40,0)
para determinarlos valores del vértice 1 y vértice 4 fue por observación de la gráfica.
para determinar el vértice 2, se observa que la restricción 1 y 3 interactuan,por lo tanto se resuelve en forma algebraica porel metodo llamado suma o resta
3X1 + X2 =171 restricción 1
X2 =120 (-) restricción 3 se mutiplica por - para
eliminar X2 al sumarlo
3X1 + X2 =171 restricción 1
-X2 =-120 restricción 3
__________________
3X1 = 51 despejando X1
X1 = 51/3
X1=17 sustituir X1 en la restricción 1
3X1 + X2 =171
3(17) + X2 =171
51 * X2 = 171
X2=171/51
X2=120
vertice 2 =(17,120)
para determinar el vértice 3, se observa que la restricción 1 y 2 interactuan,por lo tanto se resuelve en forma algebraica por el método llamado suma o resta
3X1 + X2 = 171 se multiplica por -3 para eliminar X1
X1 = 40 (-3)
3X1 + X2 = 171
-3X1 =-40
___________________
X2=51
vértice 3= (40,51)
en la función objetivo se sustituyen los valores de X1 y _X2 de los vértices para comparar las coordenadas de los vértices y escoger el optimo
Maximizar Z = 2X1 + 1.4X2
vértice 1 (0,120) 2(0) + 1.4(120)= 168
vértice 2 (17,120) 2(17) + 1.4(120)= 202 <-optimo
vértice 3 (40,51) 2(40) + 1.4(51)= 151.4
vértice 4 (40,0) 2(40) + 1.4(0)= 80
17 y 120
se multiplican las cantidades por 100 por que estan en horas maquina
17*100= 17000 artículos del modelo A
120*100= 12000 artículos del modelo B
$202 *100 = $20200 de utilidad
atte. Alejandro Del Rivero
adelrivero@hotmail.com
Este comentario ha sido eliminado por el autor.
EliminarEste comentario ha sido eliminado por el autor.
ResponderEliminartenof una duda tengo varias restricciones pero una de ellas es x-y= o en ese caso como la despejaria
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarUna fabrica tiene dos maquinas (I y II ) . La fabrica puede elegir producir el producto A o el producto B o ambos.Los productos requieren tratamiento en ambas maquinas (Sin importar el orden )
ResponderEliminarLos datos son los siguientes :
Producto Tiempo en maquina
(seg./Unidad)
I II
A 20 5
B 10 15
---------------
Costo de material
(Peso/Unidad)
A 9
B 9
------------
Precio de venta
(Pesos/Unidad )
A 15
B 13
La maquina I cuenta $ 2 el minuto y la maquina II $ 1 el minuto .Suponemos que los costos de funcionamiento de las maquinas son indepedientes de cuato tiempo esta el funcionamineto .No es muy realista pero dado que los costos son tan bajos el error es despreciable .Determinar el proceso de produccion por minuto que maximiza la
ganancia / unidad de tiempo de la siguiente forma :
a) Formular un dodelo linial.
b) Solucionar en forma grafica .
c) Solucionar con el Metodo Simplex .
ALGUIEN ME AYUDA
alguien puede ayudarnme con este ejercicio
ResponderEliminarUn ejemplo de una aplicación de programación lineal es un carpintero que hace mesas y sillas para vivir. Quiere maximizar sus ingresos netos y necesita saber cuántas mesas y sillas debe hacer por semana. Usando la programación lineal, su problema debe ser descrito con precisión, e incluir la evaluación de los costos fijos (como el costo del alquiler de su tienda) y costos variables (como las cantidades de madera y la mano de obra). Sus limitaciones son los límites en la mano de obra disponible y los tiempos de entrega de la madera y de otras materias primas. Debe establecerse un período de tiempo para el análisis, por ejemplo, una semana. Además, se haría un estudio de tiempos para medir el tiempo de producción del carpintero para producir una silla y una mesa. Utilizando cada una de estas restricciones, junto con el objetivo deseado, elabora el modelo de programación lineal y determina las cantidades óptimas aplicando el método gráfico.
alguien que me ayude:
ResponderEliminar3. Workcomp es una cadena de tiendas de servicio para computadoras. La cantidad de horas de tiempo de reparación calificada que requiere durante los cinco meses siguientes es como sigue:
Mes 1 (Enero): 6,000 horas
Mes 2 (Febrero): 7,000 horas
Mes 3 (Marzo): 8,000 horas
Mes 4 (Abril): 9,500 horas
Mes 5 (Mayo): 11,000 horas
A principios de enero, 50 técnicos calificados trabajan para Workcomp. Cada técnico calificado puede trabajar hasta 160 horas por mes. Para cumplir con las demandas en el futuro, es necesario capacitar a nuevos técnicos. Toma un mes capacitar un nuevo técnico. Durante el mes de capacitación, un técnico experimentado debe supervisar al aprendiz durante 50 horas. Cada técnico experimentado gana $20,000 al mes (incluso si no trabaja las 160 horas completas). Además, durante el mes de entrenamiento, el aprendiz recibe $10,000.
Al final de cada mes, 5% de los técnicos experimentados de Workcomp abandonan el trabajo para irse a otra empresa. Formule un modelo de programación lineal cuya solución permita a Workcomp minimizar el costo de mano de obra en el que incurre con el servicio de reparación en los cinco meses siguientes.
Me pueden ayudar a resolver este problema PORFAVOR!!
ResponderEliminarUn fruticultor dispone de 150 acres para cultivar dos productos (A y B). Un acre del producto A se poda en 1 dia y un acre del producto B en 2 dias, para la poda se dispone de 240 dias al año, la cosecha de un acre del producto A se lleva a cabo en 0.3 dias y la del producto B en 0.1 dias; para cosechar se dispone de 30 dias al año. Encuentre el numero de acres que deben platarse en cada producto para maximizar la ganancia si esta es de $140 dlls por cada acre del producto A y $235dlls por cada acre del producto B.
ESPERO PUEDAN AYUDARME,ME URGEE!!!
me pueden ayudar a resolver este problema POR FAVORR
ResponderEliminarUn fideicomiso planea invertir hasta 6000 millones en series de bonos: A y B. El
bono A es más seguro que el B y tiene dividendos de 8 por ciento, mientras los del
bono B son del 10 por ciento. Suponga que el reglamento del fideicomiso establece
que no deben invertirse más de 4000 millones en el bono B y que al menos deben
invertirse 1500 millones en bonos A.
a) ¿Cuánto dinero debe invertirse en cada tipo de Bono para maximizar el
rendimiento? (Resuelva el modelo por método grafico)
Si el fideicomiso tiene la ‘siguiente regla adicional: “La cantidad invertida en el B
no puede ser mayor que la mitad de la cantidad invertida en el bono A”.
b) ¿Cuánto dinero debe invertirse en cada tipo de bono para maximizar el
rendimiento? (Resuelva el modelo por método Símplex) R
me pueden ayudar a resolver este problema POR FAVORR
ResponderEliminarUn fideicomiso planea invertir hasta 6000 millones en series de bonos: A y B. El
bono A es más seguro que el B y tiene dividendos de 8 por ciento, mientras los del
bono B son del 10 por ciento. Suponga que el reglamento del fideicomiso establece
que no deben invertirse más de 4000 millones en el bono B y que al menos deben
invertirse 1500 millones en bonos A.
a) ¿Cuánto dinero debe invertirse en cada tipo de Bono para maximizar el
rendimiento? (Resuelva el modelo por método grafico)
Si el fideicomiso tiene la ‘siguiente regla adicional: “La cantidad invertida en el B
no puede ser mayor que la mitad de la cantidad invertida en el bono A”.
b) ¿Cuánto dinero debe invertirse en cada tipo de bono para maximizar el
rendimiento? (Resuelva el modelo por método Símplex) R
me pueden ayudar a resolver este problema POR FAVORR
ResponderEliminarUn fideicomiso planea invertir hasta 6000 millones en series de bonos: A y B. El
bono A es más seguro que el B y tiene dividendos de 8 por ciento, mientras los del
bono B son del 10 por ciento. Suponga que el reglamento del fideicomiso establece
que no deben invertirse más de 4000 millones en el bono B y que al menos deben
invertirse 1500 millones en bonos A.
a) ¿Cuánto dinero debe invertirse en cada tipo de Bono para maximizar el
rendimiento? (Resuelva el modelo por método grafico)
Si el fideicomiso tiene la ‘siguiente regla adicional: “La cantidad invertida en el B
no puede ser mayor que la mitad de la cantidad invertida en el bono A”.
b) ¿Cuánto dinero debe invertirse en cada tipo de bono para maximizar el
rendimiento? (Resuelva el modelo por método Símplex) R
Buenas tardes,me pueden ayudar con este ejercicio?.
ResponderEliminarUna empresa de transporte dispone 10 buses que realizan recorrido por distintas provincias según contrato. En un día cualquiera, 6 buses están en un punto B, uno está en el punto A y 3 en C. Por otro lado, se tiene un pedido de 5 buses en el punto De y 4 en la localidad E. El único costo para la empresa es el transporte de los buses a los puntos requeridos y está en función a la distancia que deben recorrer.En el siguiente cuadro se presentan los costos de transporte por bus, desde los distintos lugares en qué están ubicados hasta los puntos en qué se los requiere.
Localidades A B C D E
50$ 60$ 30$ 80 40 20
se va a organizar una planta de un taller de automóviles donde van a trabajar electricistas y mecánicos por necesidades de mercado, es necesario que haya mayor o igual numero de mecanicos que de elecrisista y que el numero de mecanicos no supere al doble que el de electrisista . en total hay disponibles 30 electrisista y 20 mecanicos . elbeneficio de la empresa por jornada es de 250 euros por electrisista y 200 euros por mecanico ¿cuantos trabajadores de cada clase deben elegirse para obtener el maximo beneficio y cual es este
ResponderEliminarBuenas tardes me pueden ayudar con este ejercicio
ResponderEliminarUna aerolinea ofrece vuelos de la Ciudad de Mexico a Nueva York para clientes regulares al precio de 10.000 pesos y a clientes VIP al precio de 6.000 pesos. A los clientes VIP se le deja llevar 50 kg. de peso y a los clientes regulares 20 kg. Si el vuelo tiene 90 asientos disponibles y admite un equipaje de hasta 3.000 kg. ¿Cuál ha de ser la oferta de vuelos de la compañía para cada tipo de cliente, con la finalidad de optimizar el beneficio?
minimizar z=20x+30y
ResponderEliminarsujeta a
2x+y<=(menor o igual)10
3x+4y<=(menor o igual)24
8x+7y>= (mayor igual)56
x,y>=0
HOLA...¿Alguien me puede ayudar a este problema?
ResponderEliminarA continuación, se presenta una dinámica para argumentar a favor o en contra sobre una situación:
Juan tiene una fábrica de chocolates en donde produce más de cien mil productos al día. Hoy le llegó un pedido especial y no recordó que le tocaba mantenimiento preventivo a 4 de sus 7 máquinas, por lo cual sólo contará con las máquinas M1, M2 y M3 para realizar el trabajo y poder cumplir con el pedido en tiempo.
T1 T2 T3
M1 1 2 3
M2 2 4 6
M3 3 6 9
Para poder cumplir con el pedido Juan ha expresado el problema como uno de transporte y como programación lineal para poder analizar la situación. A continuación, se muestran las soluciones que ha podido obtener:
A) Haciendo 1 de las cantidades de suministros y demandas se tiene la tabla del problema de transporte balanceado.
B) Sea XIJ = 1 o 0, según que la máquina i realice la tarea j o no.
El problema de programación lineal es:
Comparte tu opinión:
1. ¿Qué es lo que descubre Juan al momento de realizar los dos análisis?
2. ¿Es correcto asumir que las variables toman los valores 1 o 0?
3. ¿Qué papel juegan las restricciones de igualdades para que asumamos que los valores son 1 o 0?
hola pudiste resolver el problema??? es que me lo estan solicitando en una actividad
EliminarBuen día estimada patricia, lograste resolver este caso?
EliminarHola
ResponderEliminarMe podrían ayudar con este problema?
CASO:
Cremitas S.L. Caso La empresa Cremitas S.L. se dedica a la producción, el transporte y la comercialización de cremas para el cuidado de la piel. Actualmente, la empresa está planificando la producción del próximo trimestre. Ellos han identificado que pueden producir en dos turnos diurnos y, si necesita ampliar su capacidad, puede abrir un turno nocturno. La capacidad de producción mensual, en horario diurno es de 10,850 ud/mes, mientras que, en horario nocturno, la capacidad mensual de producción es de 7,750 ud/mes. La demanda mensual es de 12,000 ud el primer mes, 13,500 ud el segundo mes y 14,500 ud el tercer mes. Los costes de producir una unidad en el turno diurno son de 15 $/ud y en el turno nocturno, de 25 $/ud. Si se desea, se puede poner en stock el producto de un mes para meses posteriores, a un coste de 8 $/ud-mes. No se dispone de stock inicial ni se desea crear stock final.
Instrucciones:
Elabora el siguiente análisis de la producción
a. ¿Cuál es el plan de producción óptimo?
b. ¿Cuál es el coste de este plan de producción?
c. ¿Cuál sería el coste del plan de producción si la capacidad de producción en en horario diurno del mes 2 aumentara en 50 unidades?
d. ¿Cuál sería el coste del plan de producción si el coste de almacenaje fuera de 10$/ud-mes?
e. ¿Cuánto aumentaría el coste del plan de producción si hubiera que guardar en stock 40 unidades para el mes 4?
hola paty, pregunta si pudiste solucionar el problema del caso
Eliminarhola patricia, pudiste resolver este ejercicio? gracias
Eliminaralguien pudo resolver este caso
EliminarALGUIEN PUDO RESOLVERLO
EliminarEl almacén D1, desea liquidar en una de sus categorias que maneja 200 productos congelados (pescado) y
ResponderEliminar100 productos lácteos (quesos) el semestre pasado. Para ello el almacén lanza dos ofertas A y B. La oferta
A consiste en un lote de pescado y uno de queso, que se vende a $50.000. La oferta B consiste en 3 lotes
de pescado y 1 de queso y se vende igual a la oferta A. No se desea ofrecer menos de 20 lotes de la oferta
A, ni menos de 10 lotes de la oferta B.
1. ¿Cuántos lotes ha de vender el almacén D1 para maximizar las ganancias?
2. ¿Qué ganancia máxima tiene en liquidar estas categorías el almacén D1?
Ejercicio (Códigos Impares)
Igualmente, los almacenes D1 preparan un paseo para 400 empleados que tienen en una zona del país. La
empresa de transporte que contratan tiene autobuses pequeños de 40 asientos y de autobuses grandes de
50 asientos, pero dispone de más de 9 autobuses. El alquiler de un autobús pequeño cuesta $40.000 y el de
uno grande $60.000.
1. ¿Calcular cuántos autobuses de cada tipo hay que utilizar para que el paseo resulte lo más económico
posible?
2. ¿Cuál es el costo del transporte mínimo que debe pagar los almacenes D1, para llevar a sus empleados a
Me pueden ayudar con ese ejercicio Meda un error no lo encuentro
ResponderEliminar1. Para el siguiente gráfico realice, suponiendo que cada espacio representa 10 unidades. (35p)
ResponderEliminar1.1. Escriba las desigualdades con sus signos correspondientes ( o ) (para el área A)
1.2. Si el área incluye también a la B, qué pasa con la recta r. ¿Es necesaria? Explique.
2. Para las siguientes rectas construya el gráfico correspondiente y diga cómo es el área generada. (30p)
L1: 2x + 3y 24; L2: y 6; L3 : x 10.
3. Escriba las rectas que se muestran en el gráfico (35p)
porfavor urgente
ResponderEliminar1. En la siguiente tabla, identifique: (20p)
i. Cuántas restricciones hay
ii. Las soluciones básicas y su valor actual;
iii. Las soluciones no básicas y su valor actual;
iv. El valor de la función objetivo actual.
2. A partir de la tabla anterior: (30p)
i. Es posible otra iteración? Por qué?
ii. Si es así, qué variable entra? Por qué?
iii. Qué variable sale? Por qué?
iv. Reescriba la función objetivo algebraicamente.
3. Para el siguiente programa lineal (50p)
Resuélvalo mediante simplex
3. Escriba las rectas que se muestran en el gráfico (35p)
ResponderEliminarun artesano fabrica dos tipos de contenedores A y B hacer un contenedor tipo A le lleva dos hora y hacer el tipo B una hora el material de que dispone no le permite hacer mas de 5o contenedores como muchos el artesano puede dedicar al trabajo 80 horas por cada contenedor tipo A gana 5 y por cada contenedor de tipo b 4 el artesano desea determinar el numero de contenedores de tipo a y b que deben fabricar para optimizar su benefio
ResponderEliminar1exprese ña funsión objetivo y las restricciones del problema
2represente Graficamente el recinto definido
3 obtengase el numero de contenedores tipo a y B corresondiente al maximo beneficio
Supóngase que eres dueño de una empresa de cervezas donde solo se producen dos tipos
ResponderEliminarde cervezas: clara y obscura. El precio al mayoreo de 1000 litros de cerveza clara es de $5000
mientras que el precio al mayoreo de 1000 litros de cerveza obscura es de $3000. Un estudio
de tiempos y movimientos ha demostrado que para producir 1000 litros de cerveza clara se
requiere un total de 3 obreros en el proceso de producción. En cambio, se requieren 5
obreros para producir 1000 litros de cerveza obscura. Se supone que la planta tiene un total
de 15 obreros. Se supone que producir 1000 litros de cerveza clara le cuestan al dueño de
la planta $500, mientras que 1000 litros de cerveza obscura le cuestan solamente $200. Su
capital no le permite gastar más de $1000 semanales.
Suponga que una empresa produce chaquetas y bolsos de mano de cuero. Una chaqueta
ResponderEliminarrequiere 5 m2 de cuero, y un bolso de mano utiliza solo 3 m2. Los requisitos de mano de
obra para una chaqueta y un bolso de mano son 10 horas y 9 horas, respectivamente. El
suministro diario de cuero es de 150 m2, y el tiempo de mano de obra diario disponible es
de 360 horas. La ganancia por chaqueta es de $80, y por bolso de mano es de $50 pesos.
¿Cuáles son los mejores niveles diarios de producción para chaquetas y bolsos de mano?
The Electrocomp Corporation manufactura dos productos eléctricos: acondicionadores de
ResponderEliminaraire y grandes ventiladores. El proceso de ensamble para cada uno es similar en que ambos
requieren de una cierta cantidad de cableado y barrenado. Cada acondicionador de aire
lleva 3 horas de cableado y dos horas de barrenado. Cada ventilador debe pasar a través de
dos horas de cableado y una hora de barrenado. Durante el siguiente periodo de
producción, están disponibles 240 horas de tiempo de cableado y se pueden utilizar hasta
140 horas de tiempo de barrenado. Cada acondicionador de aire vendido genera una
utilidad de 25 dólares. Cada ventilador ensamblado puede ser vendido con una utilidad de
15 dólares. Formule y resuelva esta situación de mezcla de producción por programación
lineal, y encuentre la mejor combinación de acondicionadores de aire y ventiladores que
genere la utilidad más alta.
alguien me ayude porfa
ResponderEliminarLa empresa FRUTOS DEL CAMPO SAC, produce y exporta palta procesada
principalmente a los mercados de Chile, Estados Unidos y España, esta empresa le
presenta los siguientes datos:
Ventas totales de sus tres productos de 500,000 kilos de palta procesada
con una mezcla de ventas en kilos de 30% Chile, 28% EE. UU. y 42%
España
Gastos de exportación son el 4.5% de sus ventas
Costo variable unitario son de S/0.7, S/0.78 y S/0.88 por kilo respectivamente
La razón del margen de contribución (RMC) por cada mercado es: Chile
25%, EE. UU 30% y España 40%
Margen operativo total (utilidad operativa / ventas) 20%
Impuesto a la renta 29.5%
.
ResponderEliminarUna panadería produce dos tipos de guaguas de
ResponderEliminarpan: pequeña y grande. Para elaborar la guagua
pequeña, se necesita una hora; para la guagua
grande, tres horas. Cada guagua también debe
ser decorada. Para decorar la guagua pequeña,
se necesita una hora; para la guagua grande,
también una hora. La panadería dispone para
decorar de 2 horas y 5 horas para la elaboración.
La ganancia por unidad es de $ 2 para la guagua
de pan pequeña y $ 3 para la grande. ¿Cuál sería
la planificación de producción para obtener un
máximo beneficio?