Como Graficar Rectas Tangentes y Normales con Wolfram Alpha

Encontrar las rectas tangentes y normales de una función es uno de los ejercicios más comunes en cualquier curso de cálculo. En este post, te voy a mostrar la nueva funcionalidad de Wolfram|Alpha para descubrir e investigar sobre ellos.

El ejemplo más simple de la tangente es la "recta tangente" a una curva unidimensional en el plano. Gráficamente, la recta tangente es una línea que "sólo toca" la curva en un punto, por lo que si se mueve ligeramente, este punto de contacto se convierten en dos.

Si le preguntas a Wolfram|Alpha por la recta tangente a una función en un punto especifico, te responde tanto en forma gráfica y algebraica/numérica:

Tenga en cuenta que cerca del punto de tangencia, la recta y la curva son casi idénticas, la recta  casi se sobrepone a la curva en ese punto. Las tangentes son importantes: porque a menudo es mucho más fácil contestar preguntas acerca de las funciones lineales, y las tangentes proporcionan una forma de aproximarse a una relación complicada con una relación lineal (una línea o un plano). Es también la razón por la tangente se llama "linealización" o "aproximación lineal" de la relación.

Por ejemplo, supongamos que usted necesita saber la raíz cuadrada de 3,9. Un cálculo muy aproximado sería de 2, ya que 3,9 es aproximadamente 4, y 2 = sqrt (4). Aún mejor sería linealizar la función y = sqrt (x) en el punto x = 4, y usar esto para encontrar una estimación:

Esto indica que la aproximación lineal a sqrt (x) en x = 4 es x/4 + 1. Poner x = 3.9 en esta aproximación nos dará 3.9/4 + 1 = 1.975, que es un valor muy cercano al valor real de la raíz cuadrada de 3.9, un número irracional que los seis primeros dígitos son 1.97484

También puede pedir a Wolfram|Alpha la pendiente de una recta tangente a una función en un punto, que es otra pregunta común de cálculo (en realidad es igual a la derivada de la función en ese punto).

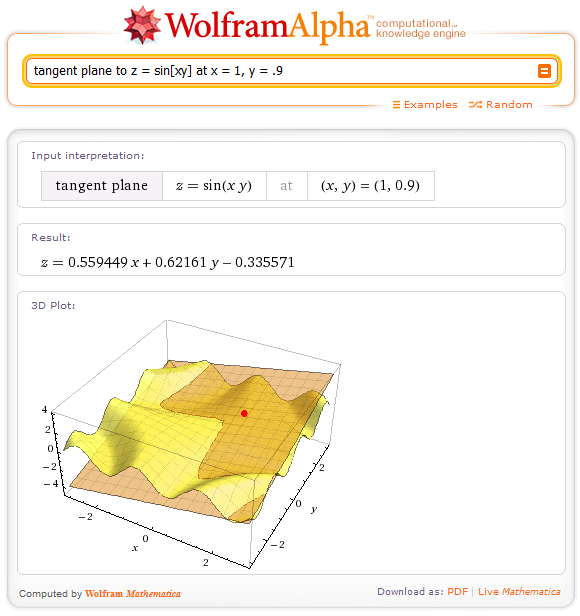
¿Qué pasa con funciones dimensiones superiores? Una función o relación con dos grados de libertad se visualiza como una superficie en el espacio, la tangente es un plano que apenas toca a la superficie en un solo punto. Por ejemplo, aquí está el plano tangente a z = sen[xy] en x = 1, y = 0.9, tal como aparece en Wolfram|Alpha:

La "normal" a una curva o superficie es una especie de complemento de la tangente. La "línea normal" en una curva unidimensional es perpendicular a la recta tangente y pasa por el mismo punto de la curva:

La normal a una superficie en el espacio es también una línea. Es la única línea que es perpendicular al plano tangente en ese punto:

Tangentes y normales a las superficies de dimensiones superiores existen también. Por supuesto, ningún argumento es posible, pero Wolfram | Alpha le dará las representaciones algebraicas y numéricas de la tangente y normal a una superficie multidimensional y cualquier punto:

Fuente y más información.

Palabras de búsqueda: como hallar rectas tangentes a una curva online, pagina para calcular online la recta tangente a una función, aplicación para determinar una recta normal a una función, pagina para graficar la recta tangente y norma, ejercicios resueltos.