Página para determinar el Dominio y Rango de un Función online (Wolfram Alpha)

En la página de Wolfram|Alpha se puede determinar el dominio y rango de una función pero no directamente(no hay una instrucción específica para ello). Para determinar el dominio y rango básicamente lo haremos utilizando la capacidad de Wolfram|Alpha para graficar funciones y hallar mínimo y máximos, veamos algunos ejemplos:

Hallar el dominio y rango de:  f(t)=2t²+3t+7

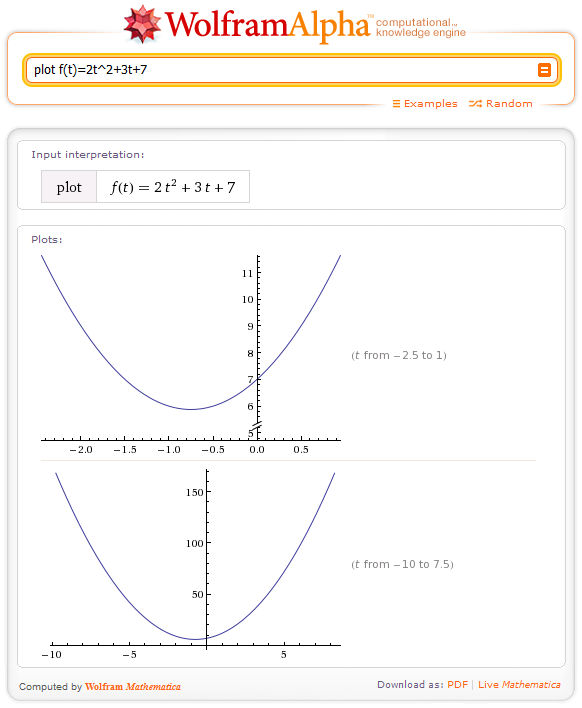
Simplemente lo que hacemos es ingresar los siguiente: plot f(t)=2t^2+3t+7, presionamos enter y luego obtenemos el gráfico de la función con lo que podemos ver fácilmente que el dominio se extiende sobre los números reales.

Para hallar el rango, debemos determinar el punto más bajo(el mínimo)  de la gráfica, entonces debemos ingresar lo siguiente:  minimize f(t)=2t^2+3t+7

Luego el rango viene dado por el intervalo: [47/8; ∞).

Veamos Otros ejemplos:

Hallar el dominio y rango de:  f(x)=√(x²-5x+4)
Ingresamos lo siguiente: plot f(x)=sqrt(x^2-5x+4), luego obtenemos el gráfico de la función:

 

Como se puede observar en el gráfico(sólo tenemos en cuenta el color azul en la gráfica que son los valores reales, el color rojo son los imaginarios) el dominio es: (-∞,1] U [4; +∞)  y el rango: [0; +∞)


Hallar el dominio y rango de:  f(x)=log((x²-4)/(2x+3))
Ingresamos lo siguiente: plot  f(x)=log10((x^2-4)/(2x+3)), luego obtenemos el gráfico de la función:

Para obtener un poco más de detalle en la figura y poder determinar el dominio de la función, restringimos el rango de visualización de la función desde -3 hasta -1 en el eje de las x, entonces ingresamos lo siguiente: plot f(x)=log10((x^2-4)/(2x+3)) from x=-3 to x=-1, luego obtenemos el siguiente gráfico:

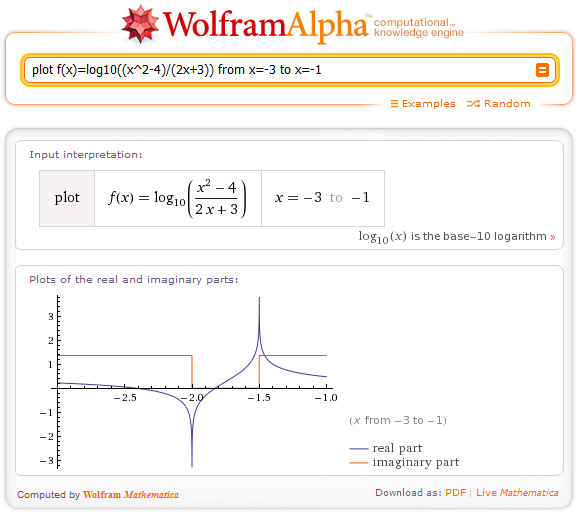
Luego viendo los dos gráficos anteriores, el dominio de la función es: (-2; -3/2) U (2; +∞),  solamente tenemos en cuenta el valor de la función donde los valores imaginarios(el color rojo en el gráfico) son iguales a cero. Como se observa el rango se extiende sobre los números reales.


Hallar el dominio y rango de:  f(x)=ln(x+1)+√(x-5)
Ingresamos lo siguiente: plot  f(x)=log(x+1)+sqrt(x-5), luego obtenemos el gráfico de la función:

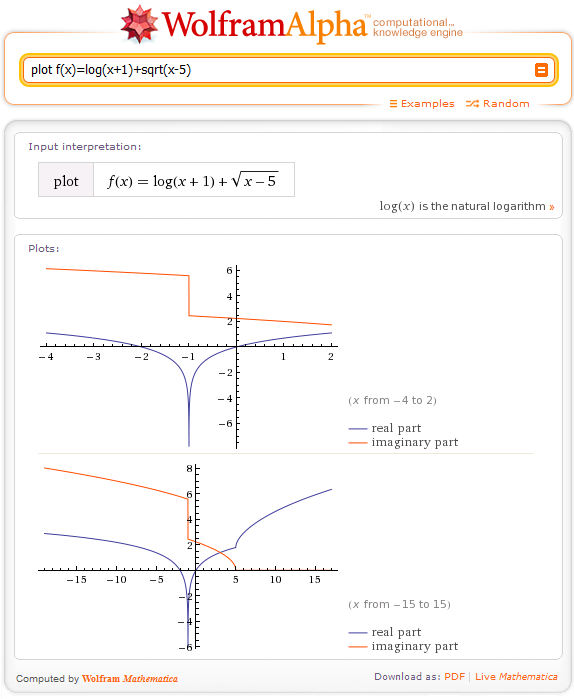
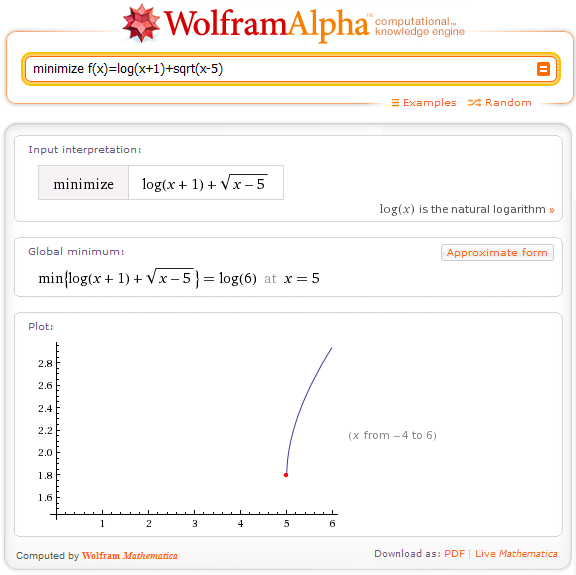
Para hallar el rango, debemos determinar el punto más bajo(el mínimo)  de la gráfica, entonces debemos ingresar lo siguiente:  minimize f(x)=log(x+1)+sqrt(x-5)

Luego, el dominio de la función es: [5;+∞) y el rango es: [ln(6); +∞)

Actualización:

Recientemente en Wolfram|Alpha han habilitado la capacidad para responder  preguntas relacionadas al dominio y rango de funciones de manera directa con palabra ... (seguir leyendo)